You're reading an old version of this documentation. For up-to-date information, please have a look at v0.12.
Analysis: Centre of mass
Classes used:
Models:
Analysis:
Processing:
Plotting:
Annotations:
In Physics, the centre of mass of a body is the mass-weighted average of the positions of its mass points. It can be equally applied to an ND dataset, where the mass is related to the intensity value at a given point.
In one dimension, the centre of mass, \(x_s\), can be calculated by:
with the total mass \(M\), i.e. the sum of all point masses:
This can be generalised to arbitrary dimensions, defining the centre of mass as the mass-weighted average of the position vectors \(\vec{r}_i\):
Recipe
Shown below is the entire recipe. As this is quite lengthy, separate parts will be detailed below in the “Results” section.
1format:
2 type: ASpecD recipe
3 version: '0.2'
4
5settings:
6 autosave_plots: False
7
8tasks:
9 - kind: model
10 type: Zeros
11 properties:
12 parameters:
13 shape: 1001
14 range: [0, 20]
15 result: dummy
16
17 - kind: model
18 type: CompositeModel
19 from_dataset: dummy
20 properties:
21 models:
22 - Lorentzian
23 - Lorentzian
24 parameters:
25 - position: 5
26 width: 0.8
27 - position: 8
28 width: 2
29 result: model_data
30
31 - kind: singleanalysis
32 type: CentreOfMass
33 apply_to: model_data
34 result: centre_of_mass
35
36 - kind: singleplot
37 type: SinglePlotter1D
38 properties:
39 properties:
40 axes:
41 xlabel: "$position$ / a.u."
42 xlim: [0, 20]
43 ylim: [0, 1.35]
44 parameters:
45 tight_layout: True
46 filename: analysis-centre-of-mass-lorentzian.pdf
47 apply_to:
48 - model_data
49 result:
50 - plot-lorentzian
51 comment: >
52 Plotter that gets annotated later
53
54 - kind: plotannotation
55 type: VerticalLine
56 properties:
57 parameters:
58 positions: centre_of_mass
59 properties:
60 color: gray
61 linestyle: dashed
62 plotter: plot-lorentzian
63 comment: >
64 Vertical line marking the centre of mass
65
66 - kind: model
67 type: Ones
68 properties:
69 parameters:
70 shape: [512, 512]
71 range:
72 - [200, 350]
73 - [275, 425]
74 result: dummy_2D
75
76 - kind: singleprocessing
77 type: Noise
78 properties:
79 parameters:
80 exponent: 0
81 apply_to: dummy_2D
82 result: model_data_2D
83
84 - kind: singleanalysis
85 type: CentreOfMass
86 apply_to: model_data_2D
87 result: centre_of_mass_2D
88
89 - kind: singleplot
90 type: SinglePlotter2D
91 properties:
92 parameters:
93 tight_layout: True
94 properties:
95 axes:
96 aspect: equal
97 filename: analysis-centre-of-mass-2D.pdf
98 apply_to:
99 - model_data_2D
100 result:
101 - plot-2D
102 comment: >
103 Plotter that gets annotated later
104
105 - kind: plotannotation
106 type: Marker
107 properties:
108 parameters:
109 positions:
110 - centre_of_mass_2D
111 marker: x
112 properties:
113 edgecolor: red
114 size: 12
115 plotter: plot-2D
Results
Examples for the figures created in the recipe are given below. While in the recipe, the output format has been set to PDF, for rendering them here they have been converted to PNG.
As this is a longer recipe demonstrating different scenarios, the individual cases are shown separately, each with the corresponding section of the recipe.
Centre of mass for 1D datasets
The scenario: We have a curve – in terms of statistics an asymmetric distribution – and want to calculate and display the centre of mass. In spectroscopy, think of an anisotropic line where you would like to get the position of the isotropic peak.
Getting the centre of mass for this asymmetric line is straight-forward and rather unspectacular:
31 - kind: singleanalysis
32 type: CentreOfMass
33 apply_to: model_data
34 result: centre_of_mass
Key here is to save the result to a variable, to be able to use the x coordinate for a plot annotation later on. This is what directly follows in the example recipe: plot the actual data and add a vertical line as plot annotation, using the result from the analysis as position:
36 - kind: singleplot
37 type: SinglePlotter1D
38 properties:
39 properties:
40 axes:
41 xlabel: "$position$ / a.u."
42 xlim: [0, 20]
43 ylim: [0, 1.35]
44 parameters:
45 tight_layout: True
46 filename: analysis-centre-of-mass-lorentzian.pdf
47 apply_to:
48 - model_data
49 result:
50 - plot-lorentzian
51 comment: >
52 Plotter that gets annotated later
53
54 - kind: plotannotation
55 type: VerticalLine
56 properties:
57 parameters:
58 positions: centre_of_mass
59 properties:
60 color: gray
61 linestyle: dashed
62 plotter: plot-lorentzian
63 comment: >
64 Vertical line marking the centre of mass
The resulting figure is shown below:

Fig. 41 Plot of an asymmetric curve with the centre of mass determined using the aspecd.analysis.CentreOfMass analysis step highlighted using a vertical line as plot annotation.
Determining the centre of mass works for arbitrary data in arbitrary dimensions, and even with non-equal spacing of the axes.
Centre of mass for 2D datasets
While determining the centre of mass works for arbitrary dimensions, we restrict ourselves here to two dimensions and use the simplest of all models: a 2D array with purely Gaussian noise. In such case, one would expect the centre of mass to be pretty much at the centre of the 2D array, and this is indeed the case, as will be demonstrated in the figure below.
Getting the centre of mass for a 2D dataset is straight-forward and identical to the 1D case:
84 - kind: singleanalysis
85 type: CentreOfMass
86 apply_to: model_data_2D
87 result: centre_of_mass_2D
Key here is again to save the result to a variable, to be able to use the coordinates for a plot annotation later on. Note that in case of 2D data, you will get two coordinates, and generally for nD data, of course n coordinates.
Marking a point in a 2D plot can be done by simply placing a marker at the respective position. For simplicity, we have used a aspecd.annotation.Marker task and placed an “x” at the centre of mass:
89 - kind: singleplot
90 type: SinglePlotter2D
91 properties:
92 parameters:
93 tight_layout: True
94 properties:
95 axes:
96 aspect: equal
97 filename: analysis-centre-of-mass-2D.pdf
98 apply_to:
99 - model_data_2D
100 result:
101 - plot-2D
102 comment: >
103 Plotter that gets annotated later
104
105 - kind: plotannotation
106 type: Marker
107 properties:
108 parameters:
109 positions:
110 - centre_of_mass_2D
111 marker: x
112 properties:
113 edgecolor: red
114 size: 12
115 plotter: plot-2D
As we got the coordinates from the analysis step, we can directly use the result in the positions key here. The resulting figure is shown below:
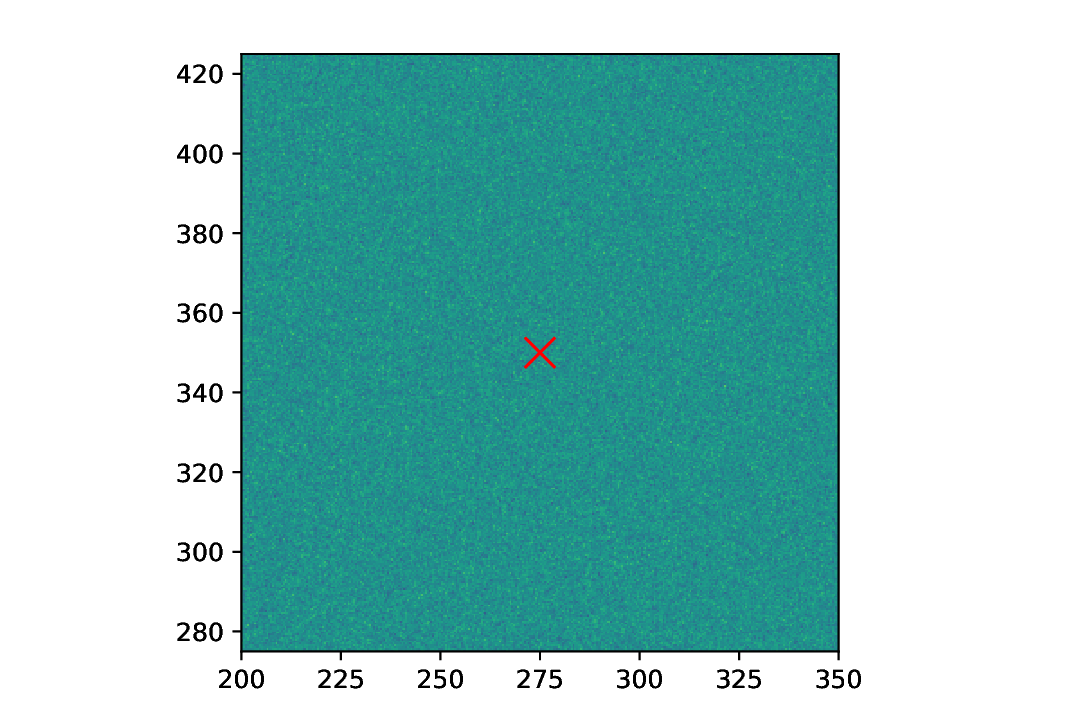
Fig. 42 Plot of a 2D dataset consisting of purely Gaussian noise. As expected, the centre of mass is pretty much at the centre of the dataset.
As the dataset has quadratic shape, we have set the aspect ratio of the plot to equal in this case, in order to not distort the individual data points.
Comments
As usual, model datasets are created, to have something to work with. Here, a CompositeModel comprising of two Lorentizans is used to get an asymmetric curve with an interesting centre of mass. For the 2D case, purely Gaussian noise is created.
For simplicity, generic plotters are used, to focus on the analysis.